Game of Machine Learning: Shapley Values for Interpretability

Contents

• Introduction
• Shapley Values
• Shapley Values and Coefficient of Multiple Determination
• Examples

Code used in the blog can be accessed on GitHub

Introduction

Back to Contents

Ever faced a problem, whereas a team you would want to divide the reward among the team members based on their contribution to the game? That is, how will you distribute the gains from a cooperative game depending on the marginal contribution by each player? Shapley values in cooperative games precisely address the issue. Shaley values applied in interpretable linear regression decouples the predictor influences in $R^2$. Each predictor is considered a player and linear regression estimation is the game they play, where the $R^2$ value is the reward they receive after the game (linear regression). If the players (predictors) are more representative of the output then the game is successful and $R^2$ values are higher. So we formalize this intuition in the following post.

Shapley Values

Back to Contents

To understand what is Shapley values and how it is related to interpretable linear regression (already intuition is given in Introduction), let’s get some definition sorted out.

Cooperative Game: is defined as a pair of $(N,v)$ with $N={1,2…,n}$ a set of players and $v: 2^N \longrightarrow \mathbb{R}$ a characteristic function , with $v(\phi)=0$.

So what’s this characteristic function?

Before the definition, let me give a famous example to explain what $v$ is. Let’s take an example of A Voting Game. Consider that the Parliament of a certain Nation has four political parties ‘1’, ‘2’, ‘3’, ‘4’ with 45, 25, 15, 12 members respectively. To pass any bill, at least 51 votes are required.

The four political parties are the players who tussle with each other (in a game) to pass a bill, depending on their political agendas and ideologies.

• $N = \{1,2,3,4\}$ (set of all players)

From the elected seats it’s not possible for a single party to single-handedly pass a bill (note the 51 seat criterion)

• $v({1}) = 0, v({2}) = 0, v({3}) = 0, v({4}) = 0$

Even if parties ‘2’ and ‘3’ form a coalation to pass bill, that would be unsuccessful as $25+15=40<51$ required seats. Using this idea, we can also formulate these v-values,

• $v({23}) = 0, v({24}) = 0, v({34}) = 0$

Now any coalation that has atleast 51 seats can pass the bill. So this can be formulated as,

• $v({12}) = v({13}) = v({14}) = v({123}) = v({124}) = v({134}) = v({234}) = v({1234}) = 1$

Now we know that different coalitions can give different results. $v(C)$ is representative of the pay off that a coalition $C$ can expect when they play the game. Now the question is that how can you distribute the gains of the game (passing the bill in this case) and attribute it to different parties. It’s clear that if party 1 is supporting the bill, it means that bill is most likely to pass (because it holds 45 seats) and hence its share in the pay off will be more.

Now lets answer this question, Whats the marginal contribution of player i, to a coalition C a.k.a $m(C,i)$?. There may be many ways to formulate this, but we will formulate it using characteristic funtion,

$$\begin{equation} m(C,i) = v(C \cup \{i\}) - v(C) \label{marginal_contribution} \end{equation}$$

For example, consider a coalition $C=\{3,4\}$ (political party ‘3’ and ‘4’). Now the new player we are adding is 1. We would like to know whats the contribution that player 1 to the coalition?

$$\begin{equation} m(C,1) = v(\{134\}) - v(\{34\}) = 1-0 = 1 \end{equation}$$

How many ways can you create a subset of players $C$ from the set $N-i$, with $i^{th}$ player being added to the coalition? The same question can be posed differently. Let’s answer that in how many permutations of all the $N-\{i\}$ players, will the players in $C$ will be placed before player $i$, with all other players in $N - C - \{i\}$ following player $i$?. See the image to better understand what’s being asked here.

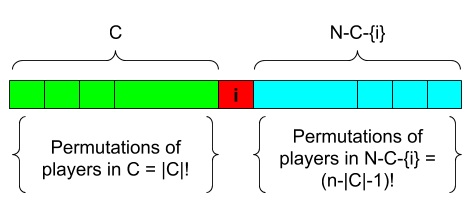
Number of permutations where the players of $C$ are ahead of player $i = |C|!(n - |C| - 1)!$. Diving this quantity with the total number of permutations $n!$, we get the probability that members of $C$ are ahead of the player $i$ in a permutation. So, the closed-form expression for Shapley values are

$$\begin{equation} SV_i = \sum_{C \subset N-i} \frac{|C|!(n-|C|-1)!}{n!}\{v(C\cup \{i\}) - v(C)\} \label{shapley_values} \end{equation}$$

But why are we finding this probability? From $\eqref{marginal_contribution}$, we get to know the marginal contribution of player $i$ when he joins a coalition of players $C$. Now, this player $i$ will make a marginal contribution to every subset of players $C$ of the total $N-i$ players, when included to that set $C$. How many ways can you choose the subset $C$ from $N-i$? (i.e) $|C|!(n-|C|-1)!$ ways and divided by $n!$ we obtain the probability of choosing the set $C$. Thus the Shapley value of resource $i$ is the average marginal contribution that player $i$ will make to any arbitrary coalition that is a subset of $N − i$.

Shapley Values and Coefficient of Multiple Determination

Back to Contents

Regression fit quality can be quantified by coefficient of multiple determination $R^2$ which is a bounded metric from $[0,1]$. Consider we have $n$ predictor variables $\left(X_1,...,X_n\right)$ and target variable $Y$. For each data point $i$, these variables assume the form $\left(x_{1i},...,x_{ni}, y_i\right)$ respectively. Now, we can formulate the linear model

\begin{equation} y_i = \beta_0 + \beta_1x_{i1}+\beta_2x_{i2}+…\beta_nx_{in}+\epsilon_i \label{genModel} \end{equation}

For now drop the constant variable $\beta_0$ (or standardize the linear regression model), and consider a model, with all the variables after they are standardized.

$$\begin{equation} y=a_1x_1+a_2x_2+...+a_nx_n+\epsilon \label{newStan} \end{equation}$$

Nows lets formulate a game! Linear regression is the game where the different predictor variables are the players. The gains we get or the characteristic function of a coalition $C$ is the $R^2_{y.C}$, (i.e) coefficient of multiple determination for the regression problem solved with a subset of variables as present in $C$.

For example consider the coalition $C=\{1,2,3\}$ of 3 players (3 predictor variables). What’s $v(C)$? It’s the $R^2$ for the regression model where the predictor variables are present in $C$.

\begin{equation} y=a_1x_1 + a_2x_2 + a_3x_3 \end{equation}

Now, lets say we add a player/predictor 4 to the above coalition $C$. $v(1234)$ is the $R^2$ for the regression model $ = R^2_{y.1234}$,

\begin{equation} y=a_1x_1 + a_2x_2 + a_3x_3 + a_4x_4 \end{equation}

According to the definition of marginal contribution $m(C,i)$ in $\eqref{marginal_contribution}$, the marignal contribution of adding predictor variable 4 to coalition $C={1,2,3}$ is

\begin{equation} m(C,4) = R^2{1234}-R^2{123} \ge 0 \end{equation}

Why greater than or equal to 0? Adding a predictor variable to a regression model cannot decrease $R^2$, Why? See my post on The In-Depth Guide to Interpretability Analysis in Linear Regression.

Now you would have got a general idea, of how we treat linear regression as a game and the predictor variable as players thereby using Shapley values to find the contributions of each predictor. Lets run through an simple yet an insightful example with $n=3, N=\{1,2,3\}$ predictor variables.

\begin{equation} y=a_1x_1 + a_2x_2 + a_3x_3 \end{equation}

What’s $SV_1$? (ie) shapley value for predictor $x_1$?

Looking back at $\eqref{shapley_values}$, we first need to define what all possible coalitions $C$ that can be present. In this case of $n=3$ predictors and our focus being on the first predictor, the following subsets/coalitions are possible.

• Case A: $C=\phi$ (No Predictor)

• Case B: $C=\{2\}, C=\{3\}$ (One Predictor)

• Case C: $C=\{2,3\}$ (Two Predictors)

The corresponding weights for Case A, B and C

• Case A: $\gamma(0) = 0!(3-0-1)!/3! = 1/3$

• Case B: $\gamma(1) = 1!(3-1-1)!/3! = 1/6$

• Case C: $\gamma(2) = 2!(3-2-1)!/3! = 1/3$

Now we are ready to answer whats $SV_1$

$$\begin{equation} SV_1 = \underbrace{\frac{1}{3}\left(R^2_{y.1}-0\right)}_{Case A} + \underbrace{\frac{1}{6}\left(\left(R^2_{y.12}-R^2_{y.2}\right)+\left(R^2_{y.13}-R^2_{y.3}\right)\right)}_{Case B} + \underbrace{\frac{1}{3}\left(R^2_{y.123}-R^2_{y.23}\right)}_{Case C} \end{equation}$$

Similarly, we can extend it to other 3 predictors. $SV_1$ is the portion contributed by predictor $x_1$ to the $R^2$ of the original model ($R^2_{y.123}$). This brings us to the last important result of the post (i.e)

$$\begin{equation} \sum_{i=1}^n SV_i = R^2_{y.123...n} \end{equation}$$

Shapley values summing up to coefficient of multiple determination makes it more interpretable $\implies$ its a decomposition of contributions of each predictor variable on $R^2$.

Examples

Back to Contents

Let’s take an example of $n=10$ predictors which are correlated (suffering from multicollinearity). Here we plot the Shapley values for each predictor.

Want the code? Head over to GitHub

Here we plot both Net effects and Shapley values for both the predictors. To know more about Net Effects look at the post Everything You Need To Know About Interpretability in Linear Regression: Net Effects. Shapley values (which are also called Incremental Net Effects) show a variety of advantages over traditional net effects. If you are interested in this, you will also be interested in The In-Depth Guide to Interpretability Analysis in Linear Regression!