Decision Making based on Expert Advice: CONSIST & Halving

Contents

• Introduction to Online Decision Making
• CONSIST Algorithm
• Halving Algorithm
• Experimental Results

Introduction to Online Decision Making

Back to Contents

Assume that you are an investor in the stock market. You have $d$ expert friends who are experts in predicting whether investing on the stock market will be profitable or not for a particular day. We assume a stock market transaction to be complete in a single day (i.e) you listen to the advice of your $d$ experts and make a decision in the morning, execute the decision by afternoon, experience the results (profit/loss) by the end of the day. This repeats every day, and you aim to minimize the total number of days you suffered losses when you engaged in a transaction. So pause a minute and think how will you approach such a problem?

Lets mathematically formulate the problem. Each expert gives his binary advice = $\{0,1\}$ to you in the beginning of the day. Here $0$ means he advices you not to invest on that day, because he is expecting a loss, when $1$, he asks you to go ahead and invest as he is expecting profit. You accumulate $d$ such advices into a vector $x_t \in \{0,1\}^d$, and then make your decision $p_t \in \{0,1\}$. Depending on the environment state (out of your control) you accept a profit or loss (consequences of your action $p_t$). You are the agent in the game. This in psuedocode format can be represented as,

    
\begin{algorithm}
\caption{Online Problem Setting}
\begin{algorithmic}
\PROCEDURE{OnlineRound}{}
    \FOR{$t = 1$ \TO $T$}
        \STATE Receive $x_t \in \{0,1\}^d$ \Comment{getting expert advice}
        \STATE Predict $p_t$ \Comment{agent makes the decision}
        \STATE Receive $y_t$ \Comment{environment gives the reward}
        \STATE Suffers $l(p_t,y_t)$ \Comment{Penalized for incorrect prediction}
    \ENDFOR
\ENDPROCEDURE
\end{algorithmic}
\end{algorithm}

One possible definition of $l(p_t,y_t)$ is,

The algorithm aims to minimize sum loss over timesteps.

Before we look into the algorithms, let’s go over some definitions to make analysis easier later.

Mathematical Notations

Back to Contents

• Agent chooses from advice of $d$ experts which is revealed to the agent in a vector form $x_t \in \{0,1\}^d$, where $x_t[i]$ is the advice of the $i^{th}$ expert.
• The true answer is received $y_t \in \{0,1\}$ (can e $[0,1]$ depending on the problem)
• Hypothesis Class (the set of functions from which the agent can choose to predict from): $\mathcal{H}$
• $h \in \mathcal{H}: x \longrightarrow \{0,1\}$ a function which maps expert advices to the predictions. We have a set of $\mathcal{H}$ of functions from which predictor can choose from.

Assumptions

Back to Contents

We assume that the environment is limited and cannot be a free adversary. What does this mean and what’s this constraint? (Note: environment and adversary are interchangeably used)

Assume in the previous example what happens when the environment/adversary decides opposite to $p_t$. That is, when the agent decides to invest, the environment ensures there is a loss, and the agent decides not to invest then the environment gives a profit which the agent missed by not investing. Under this setting, any online algorithm is meaningless as it’s bound to make a mistake because the Online Problem Setting (Algorithm 1), guarantees that the agent decides before the environment reveals the reward.

To avoid this case, we must constraint the representative power of the adversary. How do we do that? We assume that the adversary is always consistent with one of the experts. In other words we have $h^{*} \in \mathcal{H}$ which the adversary uses to generate all the target labels (loss/profit in our example) $y_t$ $(= h^{*}(x_t))$.

CONSIST Algorithm

Back to Contents

The algorithm starts with a finite hypothesis class $\mathcal{H}$. The algorihtm proceeds as follows,

    
\begin{algorithm}
\caption{CONSIST Algorithm}
\begin{algorithmic}
\PROCEDURE{CONSIST}{$\mathcal{H}$}
    \STATE $H_1 = \mathcal{H}$
    \FOR{$t = 1$ \TO $T$}
        \STATE Receive $x_t \in \{0,1\}^d$
        \STATE Choose a $h \in H_t$
        \STATE Predict $p_t = h(x_t)$
        \STATE Update $H_{t+1} = \{h \in H_t: h(x_t)=y_t\}$
    \ENDFOR
\ENDPROCEDURE
\end{algorithmic}
\end{algorithm}

This algorithm maintains a set of hypothesis functions $H_t$ that are consistent. Its a simple algorithm which says, follow a $h$ until it makes a mistake (when it will be eliminated), then choose another one in $H_t$. In experts setting, each $h$ is an expert, so the agent follows a single expert till that expert makes a mistake and then switches on to another one. In this way, we converge to the optimal $h^{*}$ (note the realizability assumption used here).

class CONSIST:
    def __init__(self,d):
        # initially all the experts are in the hypothesis class
        self.h_t=np.arange(d)
        # a binary vector to maintain the set of active predictors
        self.mask=np.ones_like(self.h_t)
        # sampling randomly a predictor from the active set
        norm_mask=self.mask/self.mask.sum()
        self.current_expert=np.random.choice(self.h_t, p=norm_mask)
        self.mistake=[]
        self.t=0
    def predict(self, xt):
        return xt[self.current_expert]
    
    def update(self, xt, yt):
        # xt is the advices of all the predictors (d-dim vector)
        # yt is the output of the adversary (scalar = 0/1)
        self.t=self.t+1
        pred=self.predict(xt)
        
        norm_mask=self.mask/self.mask.sum()
        self.current_expert=np.random.choice(self.h_t, p=norm_mask)
        # commmited a mistake!
        if(pred!=yt):
            self.mistake.append(1)
            # remove all the wrong hypothesis
            wrongIdx=np.where(xt!=yt)[0]
            self.mask[wrongIdx]=0
            # check for realizability
            if(np.count_nonzero(self.mask)==0):
                print("Non Realizable Adversary!")
                exit(0)
        else:
            self.mistake.append(0)

What’s the mistake bound of the algorithm $\mathcal{M}_{Consistent}(\mathcal{H})$?

Recall, mistake bound of algorithm $\mathcal{A}$ on a hypothesis class $\mathcal{H}$ is the upper bound on the number of mistakes it makes on $\mathcal{H}$. CONSIST algorithm has a mistake bound of

Though it’s easy to see why this is the case, it would be helpful to note that the agent eliminates a function in $\mathcal{H}$ when it incurs a mistake. The maximum number of mistakes the algorithm can make is $| \mathcal{H}| -1$, as by realizability assumption we have a $h^{*} \in \mathcal{H}$ which perfectly mimics the adversary.

Halving Algorithm

Back to Contents

Ok, let’s see where we are now. We have figured out an algorithm that can find the best expert in $O(|\mathcal{H}|)$ mistakes. Is there any algorithm that can perform better than this bound? We will see that Halving algorithm reduces the mistake bound to $O(log |\mathcal{H}|)$. It’s based on majority voting and necessarily requires finite $\mathcal{H}$.

    
\begin{algorithm}
\caption{Halving Algorithm}
\begin{algorithmic}
\PROCEDURE{Halving}{$\mathcal{H}$}
    \STATE $H_1 = \mathcal{H}$
    \FOR{$t = 1$ \TO $T$}
        \STATE Receive $x_t \in \{0,1\}^d$
        \STATE $\epsilon_0(H_t,x_t) = \{h \in H_t: h(x_t)=0\}$
        \STATE $\epsilon_1(H_t,x_t) = \{h \in H_t: h(x_t)=1\}$
        \STATE Update $p_t = \begin{cases}
            0 & if\  \|\epsilon_0(H_t,x_t)\| > \|\epsilon_1(H_t,x_t)\|, \\
            1 & otherwise
        \end{cases}$
        \STATE Update $H_{t+1} = \epsilon_{y_t}(H_t,x_t)$
    \ENDFOR
\ENDPROCEDURE
\end{algorithmic}
\end{algorithm}

In $Line:5,6$ of Halving algorihtm, we partition the active hypothesis class $H_t$ into two parts on the basis of its prediction on $x_t$. $\epsilon_0(H_t,x_t)$ are all the functions in $H_t$ which predict $0$ for the given input $x_t$ and $\epsilon_1(H_t,x_t)$ are the functions which predict $1$. The algorithm’s strategy is to go with the maximum vote, that is if the number of functions in $H_t$ predicting $0$ for given $x_t$ is higher, $(|\epsilon_0(H_t,x_t)| > |\epsilon_1(H_t,x_t)|)$, $p_t=0$, or $p_t=1$. THe update at $Line: 8$ ensures a consistent set of hypothesis class is maintained.

class Halving:
    def __init__(self,d):
        self.h_t=np.arange(d) # all the experts form the hypothesis class
        self.mistake=[]
        self.t=0
    def predict(self, xt):
        # checking for a majority and predicting based on that
        if (np.mean(xt[self.h_t]) >= 0.5):
            return 1.0
        else:
            return 0.0
    
    def update(self, xt, yt):
        self.t=self.t+1
        pred=self.predict(xt)
        if(pred!=yt):
            self.mistake.append(1)
            # checking for realizability
            if(self.h_t.shape[0]==0):
                print("Non Realizable Adversary!")
                exit(0)
            # finding the set of all the active predictors in $H_t$
            active_experts_prediction = xt[self.h_t]
            # only preserving predictors who are consistent
            # this means, majority of predictors are rejected
            rightIdx=np.where(active_experts_prediction==yt)[0]
            self.h_t = self.h_t[rightIdx]
        else:
            self.mistake.append(0)

What’s the mistake bound of the algorithm $\mathcal{M}_{Halving}(\mathcal{H})$?

Let’s answer a related question, when will this algorithm make a mistake? Say at time $t$, the algorithm commits a mistake. As the algorithm goes by majority vote, it means the majority of the functions/predictors in $H_t$ have wrong predictions for $x_t$. Therefore majority functions $(\ge |H_t|/2)$ will be eliminated at $t$.

Extending the argument, whenever the algorithm makes a mistake, at least more than half of the active hypothesis class is eliminated.

If $M$ is the total number of mistakes, then $$\begin{equation} 1 \le \|H_{t+1}\| \le \|\mathcal{H}\|2^{-M} \end{equation}$$

Similar to that of the calculation of time complexity of the binary search, we conclude that $O(log|\mathcal{H}|)$

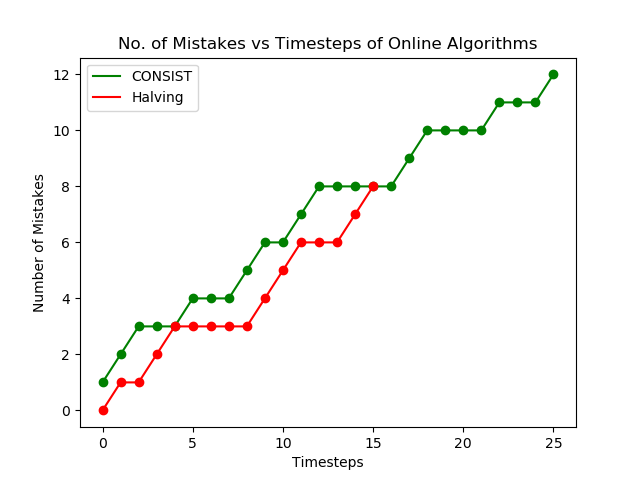
Experimental Results

Back to Contents

We create a sample dataset of around 1000 experts $(d=1000)$ and the experiment runs for $T=10000$ iterations. We use the same functions which we have shown in the algorithm’s section and we will observe the results.

What next?

Heard about VC-dimension, which is a very important concept in machine learning… it quantifies PAC-learnability. But how can we define Online Learnability? We need a new metric, which we call the Littlestone’s Dimension. Nextly, we will look into Littlestones’s dimension and its application.