A Gentle Introduction to GPU Programming using Numba

By Lokesh Kumar T

Sept 2018

IIT Madras

Overview of the Talk

• CPUs and GPUs
• Whats Heterogenous Computing?
• Introduction to GPU Programming Terminologies
• Introduction to Numba
• Lets multiply a vector by 2 in GPU!
• Matrix Multiplication in a GPU
• How to proceed further?

• CPU: work on a variety of different calculations
• GPU: best at focusing all the computing abilities on a specific task
• CPU: few cores (up to 24) optimized for sequential serial processing
• GPU: thousands of smaller and more efficient cores for a massively parallel architecture
• GPUs provide superior processing power, memory bandwidth and efficiency over their CPU counterparts.

How to exploit the Sequential Acceleration of CPU and Parallel Acceleration of GPU?

Heterogenous Computing

Basic Idea

How does GPU manage to accelerate compute intensive tasks?

• Uses parallel programming strategy
  • Breaks the tasks into several smaller sub tasks

• Many versions of the sub-tasks operating different data

• Works on the sub tasks simultaneously (parallely).

How does CPU approach this same task?

• Uses single thread. Single stream of instructions.

• Tries to accelerate that single stream of instruction.

• Sequential Processing!

What are those tasks?

Computational tasks

• Matrix Multiplications
• Vector Addition
• Fast Fourier Transforms

• Signal Processing techniques
• Deep Learning Workloads

Breaking a task into sub-tasks

• Crutial to attain maximum performance

• Depends from task to task

• Some tasks are easier and straight-forward than others

• Lets see an example

Vector Addition

• Vectors are columns of numbers

$$\vec{a} = \begin{bmatrix}1 \\2\\\vdots\\n\end{bmatrix}_{n \times 1}$$

Lets take 2 vectors $\vec{a}, \vec{b}$ both in $\mathbb{R}^n$ (n-dimensional space).

$ \vec{a} = \begin{bmatrix}a_1 \\a_2\\\vdots\\a_n\end{bmatrix} $

$ \vec{b} = \begin{bmatrix}b_1 \\b_2\\\vdots\\b_n\end{bmatrix} $

Whats $\vec{a} + \vec{b}$ ? (Vector addition)

• Element wise addition

$ \vec{a} + \vec{b} = \begin{bmatrix}a_1 + b_1\\a_2+b_2\\a_3+b_3\\\vdots\\a_n+b_n\end{bmatrix} $

for i in range(n):
    c[i] = a[i] + b[i]

How to split it into sub tasks?

In other words parallelize it?

Here are the steps (simple algorithms):

• Identify independent instructions (operations)

• Identify their input of these indepedent operations

• Finalze your fundamental unit that will have several versions running parallely.

Revisiting Visiting Vector Addition

• Whats the fundamental operation performed?
• Whats the input for this operation to be performed?

Fundamental Operation: Addition of 2 numbers

Input: One Elements from 2 vectors a[i], b[i]

Same operation is performed on different data items. (here $a[i], b[i]$)

SIMD Processing - Single Instruction Multiple Data Processing

Our Approach to program this addition in GPU:

• Replicate addition on different compute units in GPUs
• Give appropriate inputs to these units so that they perform useful operation.
• Aggregate the each units output and send it to CPU

Terminologies

• Device: GPU (Device memory: GPU Memory)

• Host: CPU (Host Memory: CPU Memory)

• Kernel: The function that runs in GPU
  • Whats our kernel in vector addition?

• Threads: The computational units in GPUs. Runs a version of the kernel.

• Blocks: Collections of a set of threads

• Grid: Collection of set of blocks

Lets Code Vector Scaling in GPU using Numba!

Sample Introduction to Numba

Numba gives you the power to speed up your applications with high performance functions written directly in Python.

We will look into a basic program and understand the Numba programming basics.

# !conda install -c numba numba
import numba

from numba import cuda
print(cuda.gpus)

<Managed Device 0>

import numpy as np
# SCALING A VECTOR BY 2
# Create the data array - usually initialized some other way
data = np.ones(256*4096) # 1,041,664

threadsperblock = 256

# Ceil function
blockspergrid = (data.size + (threadsperblock - 1)) // threadsperblock
print ("Blocks in one grid:\t" + str(blockspergrid))
print ("Threads in one Block:\t" + str(threadsperblock))

Blocks in one grid:	4096
Threads in one Block:	256

Whats this threadsperblock, blockspergrid business?

• For effective parallelization of higher dimensional data structures, loopy data structures:
  • CUDA follows an hierarchy
  • threads, blocks, grids we saw remember?

Hierarchy

• Threads: The computational units in GPUs. Runs a version of the kernel.
• Blocks: Collections of a set of threads
• Grid: Collection of set of blocks

We defined how many blocks and threads are needed.

Now lets define the kernel function

from numba import cuda

@cuda.jit
def my_kernel(io_array):
    pos = cuda.grid(1)
    if pos < io_array.size:  # Check array boundaries
        io_array[pos] *= 2 # do the computation

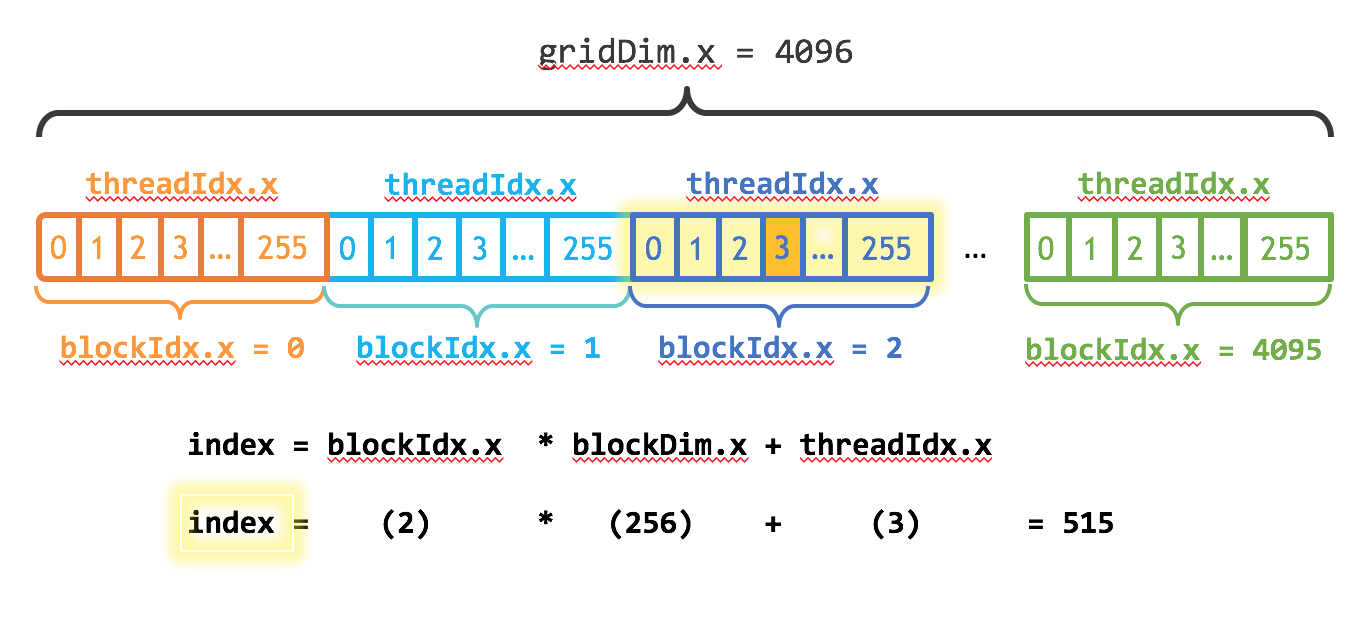
Finding the global index of the thread

• numba.cuda.grid(ndim) - Return the absolute position of the current thread in the entire grid of blocks.

Calling the Kernel from the code

%%timeit
# Now start the kernel
# And time the GPU execution time also
my_kernel[blockspergrid, threadsperblock](data)

13.6 ms ± 66.5 µs per loop (mean ± std. dev. of 7 runs, 100 loops each)

%%timeit
# timing the CPU Operations
data_2 = data*2

2.35 ms ± 278 µs per loop (mean ± std. dev. of 7 runs, 100 loops each)

Lets do Matrix Multiplication in GPU!

How will you approach this problem????

How will you assign the threads and blocks?

Remember the guidelines:

• Identify independent instructions (operations)
• Identify their input of these indepedent operations
• Finalize your fundamental unit that will have several versions running parallely.

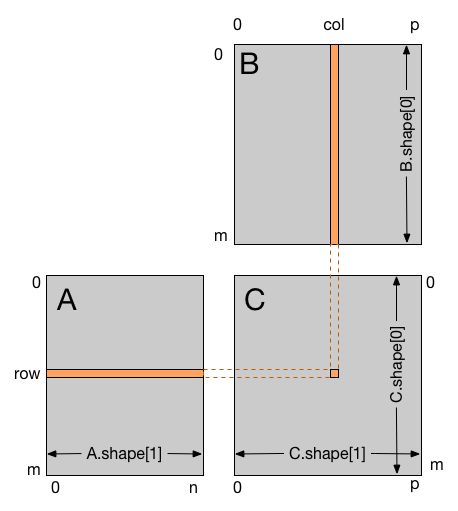
What's the dimension of the block here?

Is it 1D as we saw in scalar multiplication?

Lets code this in Numba

Host Code

# Host code

# Initialize the data arrays
m = 2**11 # 2048
n = 2**11
p = 2**11

A = np.full((m, n), 1, np.float) # matrix containing all 1's
B = np.full((n, p), 1, np.float) # matrix containing all 1's

Host to device data transfer + Memory allocation in GPU

# Copy the arrays to the device
A_global_mem = cuda.to_device(A)
B_global_mem = cuda.to_device(B)

# Allocate memory on the device for the result
C_global_mem = cuda.device_array((m, p))

Kernel

@cuda.jit
def matmul(A, B, C):
    """Perform matrix multiplication of C = A * B
    """
    i, j = cuda.grid(2)
    if i < C.shape[0] and j < C.shape[1]:
        tmp = 0.
        for k in range(A.shape[1]):
            tmp += A[i, k] * B[k, j]
        C[i, j] = tmp

Defining threadsperblock, blockspergrid

threadsperblock = (32, 32)
# Dimension of the matrix we defined is 2048x2048

blockspergrid_x = int(np.ceil(A.shape[0] / threadsperblock[0]))
blockspergrid_y = int(np.ceil(B.shape[1] / threadsperblock[1]))
blockspergrid = (blockspergrid_x, blockspergrid_y)

Kernel Call

# Start the kernel 
matmul[blockspergrid, threadsperblock](A_global_mem, B_global_mem, C_global_mem)

# Copy the result back to the host
C = C_global_mem.copy_to_host()

print(C)

[[2048. 2048. 2048. ... 2048. 2048. 2048.]
 [2048. 2048. 2048. ... 2048. 2048. 2048.]
 [2048. 2048. 2048. ... 2048. 2048. 2048.]
 ...
 [2048. 2048. 2048. ... 2048. 2048. 2048.]
 [2048. 2048. 2048. ... 2048. 2048. 2048.]
 [2048. 2048. 2048. ... 2048. 2048. 2048.]]

Lets time it!

%%timeit -n 10
matmul[blockspergrid, threadsperblock](A_global_mem, B_global_mem, C_global_mem)

299 µs ± 134 µs per loop (mean ± std. dev. of 7 runs, 10 loops each)

%%timeit -n 10
C = A.dot(B)

463 ms ± 20.4 ms per loop (mean ± std. dev. of 7 runs, 10 loops each)

New Moore's Law

• Computers no longer get faster, just Wider

• Rethink your algorithms to be parallel

• Data-Parallel Computing is the most scalable solution

Thanks for your patience

This presentation and extensive resources can be found in my GitHub - tlokeshkumar.

Even projects and other codes in GPU Programming, Deep Learning etc are present in my GitHub.... Do check them out if interested!!!

Feel free to contact me at lokesh.karpagam@gmail.com